在直流电路中，阻碍电流流动的特性被称为电阻；而在交流电路中，这种特性则被称为阻抗。阻抗以欧姆（Ω）为单位，它表示包含交流电阻和电抗的电路对电流的有效阻碍作用。在之前的教程中，我们已经了解到，在包含正弦波的交流电路中，电压和电流的相量及复数可用于表示复杂的电气量。原本在时域中绘制的正弦波形和函数可以转换到空间域或相量域，从而通过相量图建立电压与电流的相位关系。既然我们已经掌握了用相量表示电压或电流的方法，接下来将探讨这种关系在基本无源电路元件（如接入单相交流电源的交流电阻）中的应用。

任何理想的基本电路元件（如电阻器）都可以通过电压和电流进行数学描述。在关于电阻器的教程中，我们知道纯电阻两端的电压与流经的电流呈线性正比关系，即遵循欧姆定律。以下图电路为例：

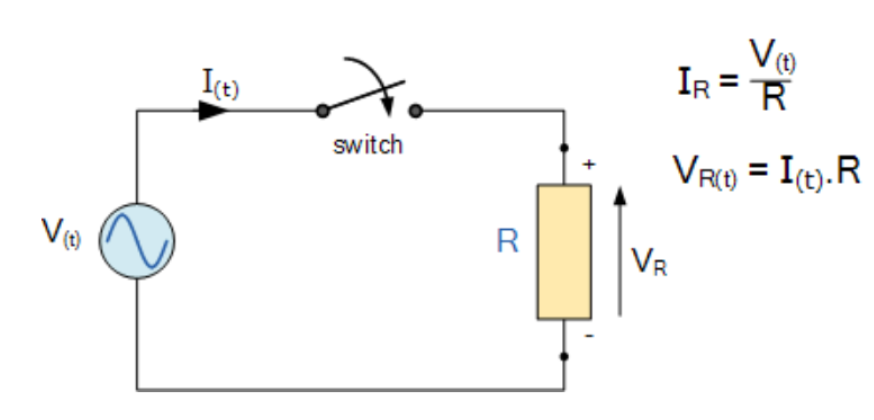
（图1：正弦电源作用下的交流电阻）

当开关闭合时，交流电压V将施加于电阻R上。该电压会产生电流，且电流会随正弦变化的电压同步升降。由于负载为纯电阻，电流和电压会同时达到峰值并同步过零，即二者“同相位”。因此，流经交流电阻的电流可表示为时变正弦函数：I(t)=Imxsin(ωt+θ)，其中Im为电流最大振幅，θ为相位角。根据欧姆定律，电阻R两端的瞬时峰值电压为：

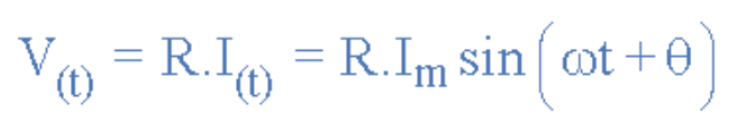
（图2：电阻R两端的瞬时峰值电压计算公式）

瞬时电流值则为：

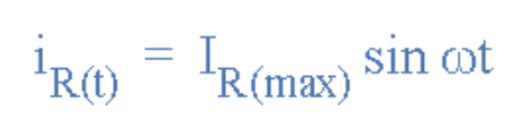
（图3：瞬时电流值计算公式）

由此可见，在纯电阻电路中，交流电流与施加电压按相同正弦规律成比例变化。由于电源频率对电压和电流相同，二者的相量完全重合，电流与电压保持“同相位”（θ=0）。也就是说，使用交流电阻时，电流与电压之间不存在相位差，电流将在电压达到最大值、最小值和零值的同一时刻实现对应值，如下图所示：

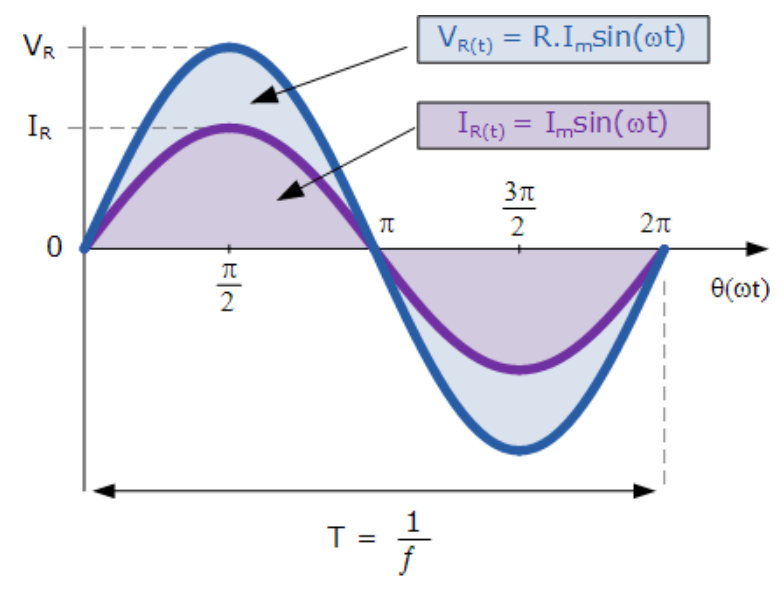
（图4：交流电阻的正弦波形）

这种“同相位”效应也可以通过相量图表示。在复数域中，电阻仅为实数（不含虚部“j”分量）。因此，由于电压和电流同相位，二者向量将沿同一参考轴重叠。相量表示的是电压和电流的有效值（RMS），而非峰值。将时域表达式的峰值除以√2后，可得电压-电流相量关系：

有效值关系：

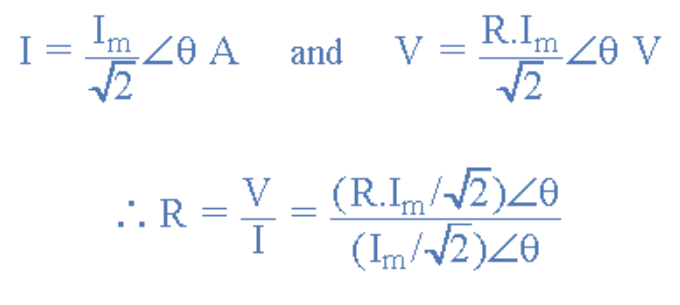
（图5：电压-电流有效值关系）

相位关系：

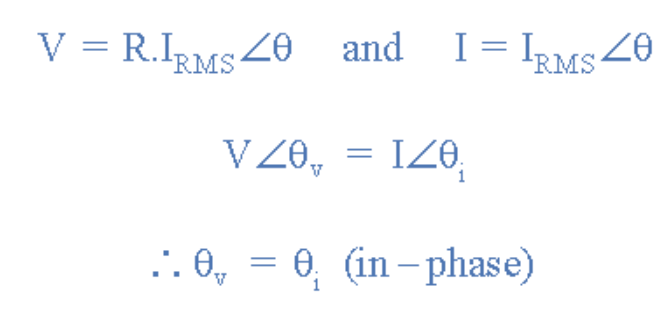
（图6：电压-电流相位关系）

这表明：交流电路中的纯电阻产生的电压-电流相量关系，与直流电路中电阻的电压-电流关系完全一致。但在直流电路中这种关系称为“电阻”（遵循欧姆定律），而在正弦交流电路中则称为“阻抗”。换言之，交流电路中的电阻即“阻抗”。

在纯电阻电路中，电压-电流（V-I）关系始终呈线性。因此，在交流电路中使用电阻时，通常用符号Z表示阻抗。可以说，对于电阻而言：直流电阻=交流阻抗，即R=Z。阻抗向量用字母Z表示，单位与直流电阻相同（Ω）。阻抗的定义式为：

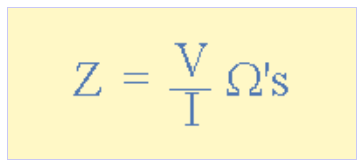
（图7：阻抗的定义式）

当电路存在无功分量时，阻抗也可用复数表示（因其与频率ω相关）。但对于纯电阻电路，虚部恒为零，其复数表达式为：

（图8：纯电阻电路的复数表达式）

施加在电阻上的瞬时交流电压和电流分别为：v=Vmsin(ωt)，i=Imsin(ωt)。由于纯电阻交流电路的相位差为零，功率因数必然为1（cos0°=1）。因此瞬时功率为：

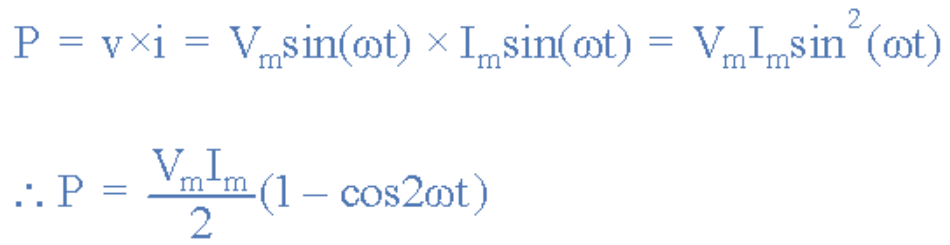
（图9：纯电阻交流电路的瞬时功率计算公式）

由于v和i同相位，cos(2ωt)项归零。电阻在一个完整周期内消耗的功率为：

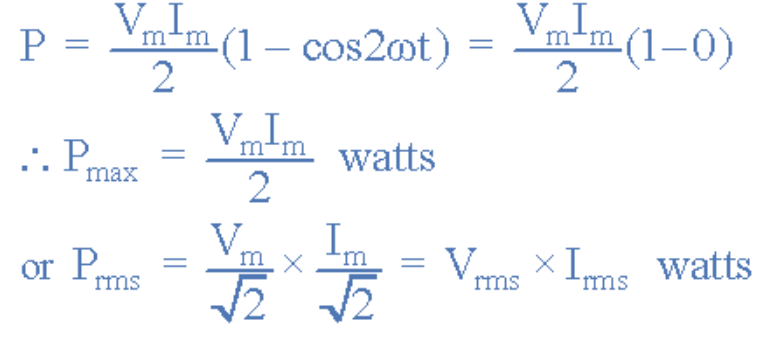
（图10：电阻在一个完整周期内消耗的功率计算公式）

在纯电阻电路中（θ=0），平均功率可直接通过欧姆定律计算：

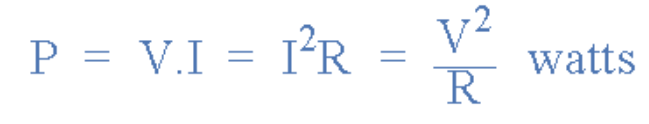
（图11：纯电阻电路的平均功率计算公式）

这与直流电路的欧姆定律公式一致。因此，交流电阻消耗的有效功率与直流电路中相同电阻的功耗完全等效——这是因为在纯电阻电路中，电压和电流始终同步，功率不会出现零值。

许多交流电路（如加热元件和白炽灯）仅包含纯电阻，其电感或电容阻抗可忽略不计。在此类电路中，我们可以像分析直流电路一样，运用欧姆定律、基尔霍夫定律等规则来计算电压、电流、阻抗和功率，且通常仅使用有效值。

接下来，我们通过两个具体实例来进一步说明交流电阻的应用。

交流电阻实例1

一个60Ω的交流加热元件接入240V有效值的单相电源。试计算电源电流和元件功耗，并绘制电流与电压相位关系的相量图。

电源电流

：

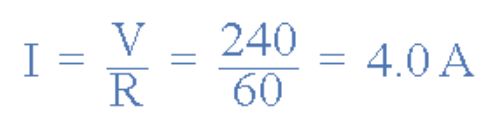
（图12：电源电流计算公式）

有功功率

：

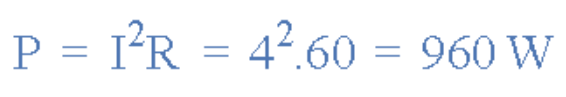
（图13：有功功率计算公式）由于无相位差（θ=0），相量图如下：

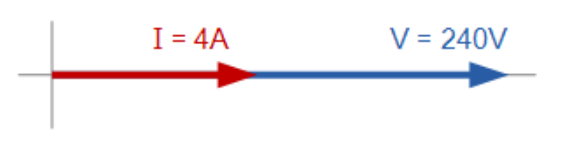
（图14：电流与电压向量同向重叠的相量图）

交流电阻实例2

某正弦电压源定义为：V(t)=100xcos(ωt+30°)，连接至50Ω纯电阻。确定其阻抗和电流峰值，并绘制相量图。

纯电阻电路的电压与电源电压相同。将时域表达式转换为相量域：

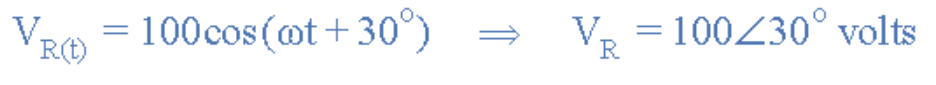
（图15：时域表达式转换为相量域）

应用欧姆定律：

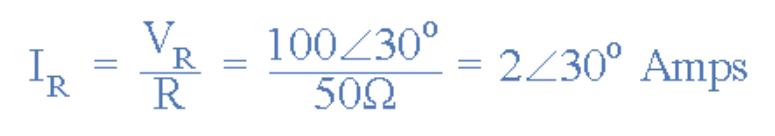
（图16：应用欧姆定律计算电流峰值）

相量图如下：

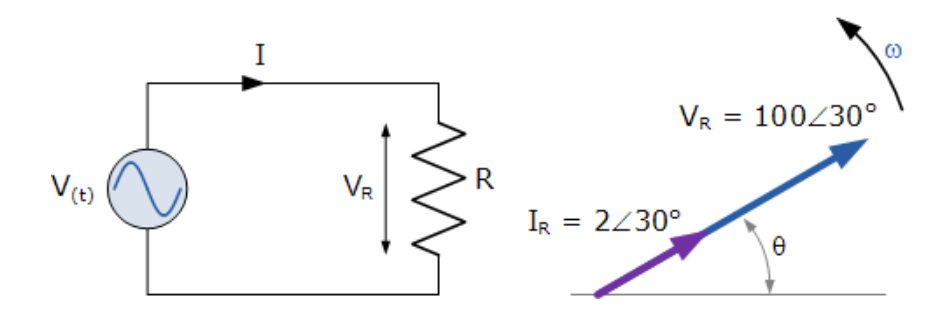
（图17：电流与电压向量均以30°角同向重叠的相量图）

综上所述，在纯电阻交流电路中，电流与电压“同相位”（无相位差）。流经电阻的电流与两端电压成正比，这种线性关系在交流电路中称为阻抗。纯电阻的阻抗Z是仅含实部（电阻值R）而无虚部（j0）的复数。因此，欧姆定律可直接用于含交流电阻的电路计算。在下一篇关于交流电感的教程中，我们将探讨稳态正弦交流波形作用下电感的电压-电流关系，并分析纯电感与非纯电感的相量图表示。