真实信号的频谱

当我们考虑将实值消息信号作为SSB波传输时，实值函数的傅里叶变换具有共轭对称性。这意味着谱的实部是偶数函数，虚部是奇数函数。如图1所示，它清晰地展示了实值基带信号频谱的实部和虚部。

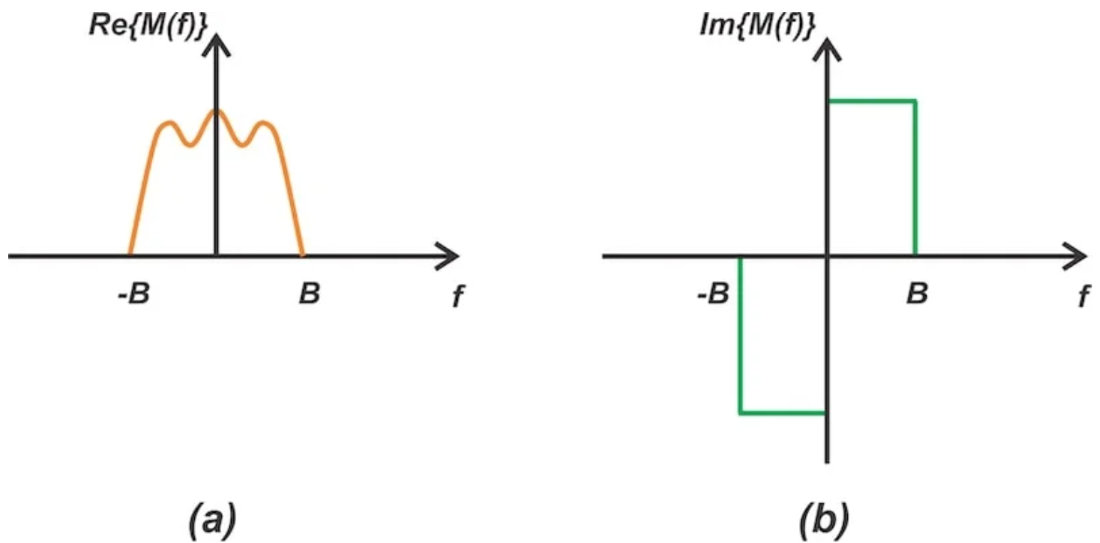
图1实值基带信号频谱的实部（a）和虚部（b）。图片由SteveArar提供

为了更直观地表示定相调制器内不同节点处的频谱，我们使用3D图来呈现上述光谱，如图2所示。

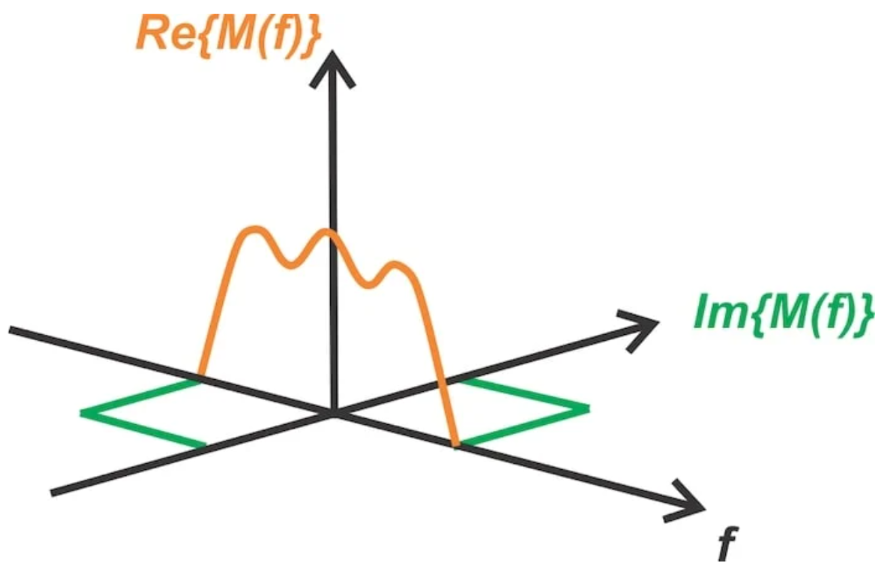
图2使用3D图演示信号频谱。图片由SteveArar提供

接下来，我们将利用这个模型来可视化希尔伯特变换。

希尔伯特变换的说明

希尔伯特变换是相位法的核心所在。正如我们在上一篇文章中所了解到的，它对应于具有特定频率响应的线性滤波器，其频率响应公式如下：

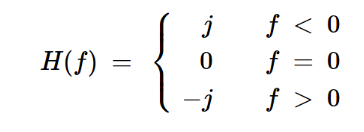
方程式1

希尔伯特变换会将所有正频率分量偏移-90度，将所有负频率分量偏移+90度，并且不影响谱振幅。由于希尔伯特变换将频率分量乘以虚数单位j，因此它会将实数分量转换为虚数分量，反之亦然。图3展示了图2中所示的频谱在经过希尔伯特变换时的变化情况。

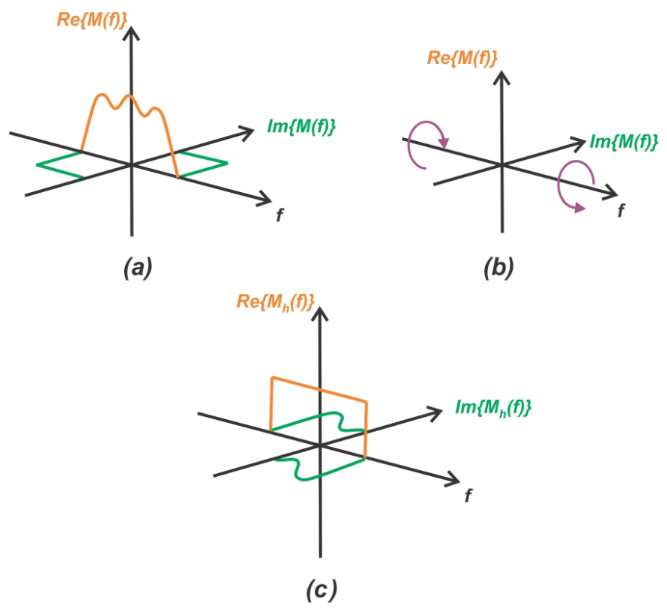
图3输入信号的频谱（a）、由希尔伯特变换引起的一个象限的空间旋转（b）和希尔伯特变换的输出频谱（c）。图片由SteveArar提供

从图中我们可以看到，希尔伯特变换将空间的正频率和负频率部分沿相反方向旋转90度。为了更清晰地理解这两个空间部分的旋转方向，我们来看几个具体的例子。

假设存在点M（f1）=1+j，其中f1是正频率，此时输入频谱的实部和虚部都是正的。由于f1是正频率分量，希尔伯特变换将该值乘以-j，得到如下结果：

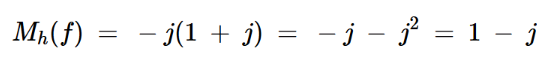
方程式2

由此可知，该频率点的输出应具有正实部和负虚部，这与图3（b）是一致的。

接下来，我们考虑一个具有正实值和负虚值的负频率分量（f2）：M（f2）=1-j，这一点对应于图3（a）的负频率部分。希尔伯特变换将产生：

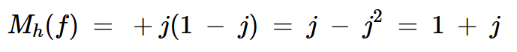
方程式3

在这里，输出的实部和虚部都是正的，这再次与上图相符。

移相特性与相位调制器

在了解了希尔伯特变换如何改变输入频谱之后，我们来进一步理解相位调制器的操作。这需要我们复习傅里叶变换的一个重要性质——移位属性。移位属性指出，将时域信号乘以复指数可以得到以下结果：

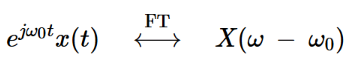
方程式4

其中，x（t）是时域信号，X（f）是X（t）的傅里叶变换，ω0是一个恒定的频率。也就是说，频谱会偏移一个恒定的频率（ω0）。

基于上述原理，我们来检查图4中的相位调制器框图。

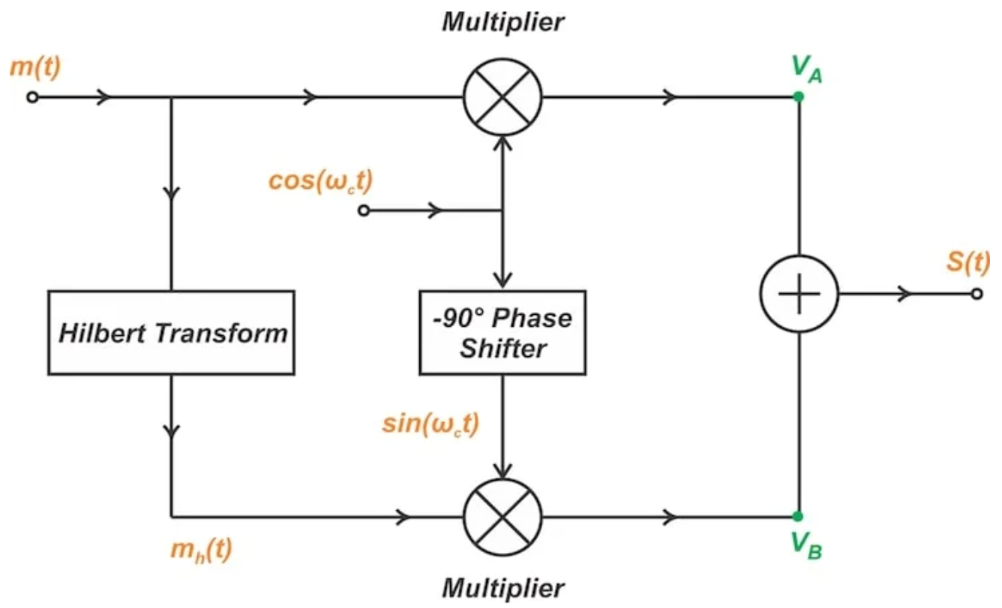
图4SSB定相方法的功能框图。图片由SteveArar提供

图中VA和VB分别表示上、下路径输出端的信号，我们也将图上的这两点称为节点A和节点B。

首先看上部信号路径，使用欧拉公式，余弦本振子波cos（ωct）可以表示为：

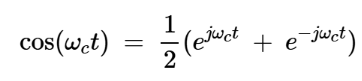
方程式5

基于移位特性，图4中的上乘法器将消息频谱转换为±ωc，并将幅度缩放0.5倍。图5（a）中可以看到结果的频谱（没有幅度缩放）。

同时，输入到下路径本地振荡器的正弦波可以表示为：

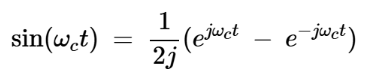
方程式6

下路径将消息信号的希尔伯特变换与上述复指数项混合，得到VB。为了帮助我们直观地理解这一点，在继续之前，我们来看图5（b）中的VB频谱。

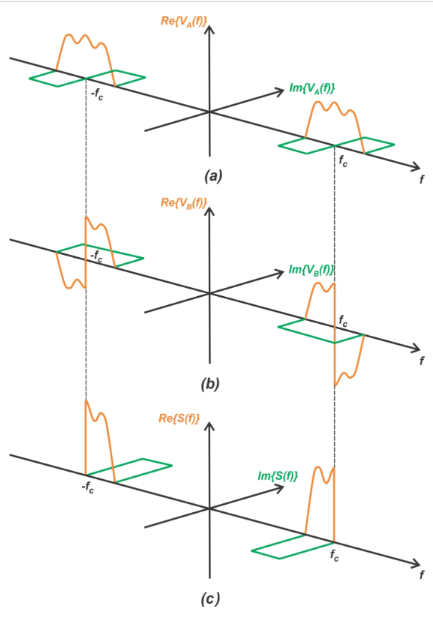
图5由上乘法器（a）产生的频谱、由下乘法器（b）产生的光谱和由输出加法器（c）产生的组合频谱。图片由SteveArar提供

方程6中的第一项将希尔伯特变换的输出谱（图3（c）中的Mh（f））移动到ωc的中心，缩放因子为1/2j。除以虚单位j对应-90度的相移，产生图5（b）中输出谱的正频率部分。除以j也会改变实部和虚部的作用，Mh（f）的实部在节点B处转换为虚部，虚部转换为实部。

方程6中的第二个指数项将希尔伯特变换的输出谱移动到-ωc，并将其缩放为-1/2j=j/2。仅考虑缩放因子j，我们观察到输出光谱偏移了+90度。在我们的3D表示中，这对应于一个象限沿顺时针方向的空间旋转。同样，空间旋转一个象限会将实部变为虚部，反之亦然。

调制输出频谱

调制器电路通过将节点A和B的频谱相加来产生输出，在这种情况下，得到的是下边带信号。如果我们用减法器替换电路输出端的加法器，它将产生上边带。

下侧带具有相同的振幅和极性，将它们加在一起会得到一个比例因子为2的输出，如图5（c）所示。对于上边带，实部和虚部的振幅相同，但极性相反，这一增加会抵消它们。

理解分段法的其他方法

在本文中，我们研究了消息信号的实部和虚部，以及相位调制器电路对它们的修改。然而，对定相方法的一些解释只考虑了信号频谱的实部。

例如，图6摘自ThomasH.Lee的《CMOS射频集成电路的设计》，它展示了真实部分在通过电路时是如何变化的。

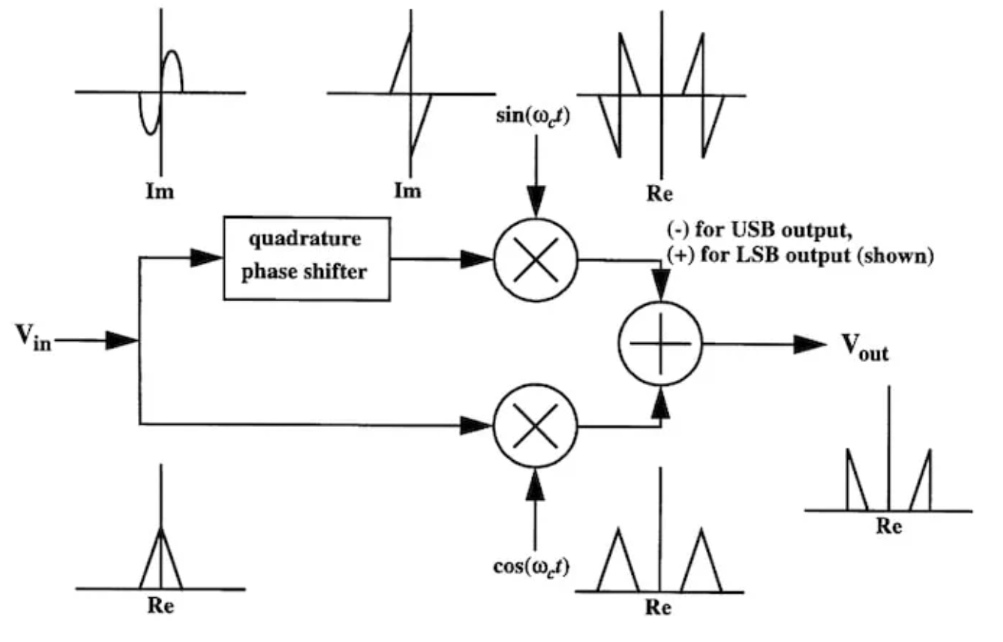
图6当只考虑输入频谱的实部时，SSB信号生成的定相方法。图片由ThomasH.Lee提供

虽然这种方法简化了电路操作的解释，但对定相方法的彻底分析应该包括频谱的实部和虚部。现在你已经探索了这个SSB电路的详细解释，作为练习，尝试验证李博士图表中所示的不同光谱。

综上所述，通过运用可视化的方法，我们能够更清晰、深入地理解SSB调制相位方法，为进一步研究和应用这一技术奠定了坚实的基础。