热电偶原理全知道：塞贝克效应和塞贝克系数详解-捷配DataSheet查询网

在温度测量领域，热电偶是当今最为常用的温度传感器之一。它由两端焊接在一起的两个不同导体组成，利用塞贝克效应来实现温度的测量。本文将深入探讨塞贝克效应以及塞贝克系数，为后续关于热电偶的详细讨论奠定坚实基础。

塞贝克效应简史

早在1822年，德国物理学家托马斯・塞贝克就有了一个意外的发现。他注意到，当由两块半圆形铋和铜连接而成的环上存在温度梯度时，这个环竟然可以使附近的指南针发生偏转（如图1所示）。当时，塞贝克的朋友汉斯・克里斯蒂安・奥斯特在1820年已经发表了他对电和磁之间联系的发现，奥斯特建议，针的移动应该是由流过回路的电流产生的磁场导致的。这便是热电效应的首次发现。不过，在当时，要为这一观察到的物理现象构建一个解释理论并非易事，因为像电压、电流和电阻等基本概念都还没有得到明确的表述。实际上，直到1897年电子被发现之后，人们才真正深入理解了这种现象的内在机制。值得一提的是，动物电的发现者路易吉・伽伐尼在1786年进行的实验也与塞贝克效应相关。当时，伽伐尼观察到，被解剖的青蛙的肌肉在被不同的金属探针接触时会出现收缩现象。

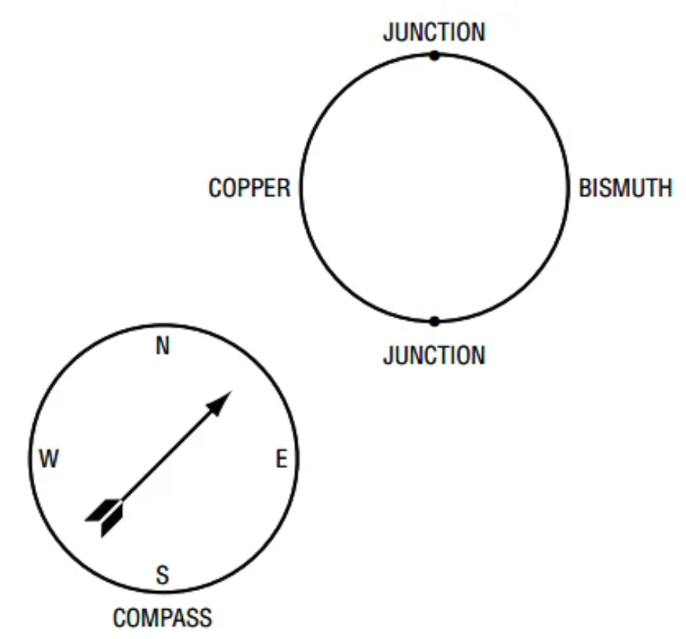
（图注：塞贝克意外发现的热磁高级代表。图像由AnalogDevices和LinearTechnology提供）

温度对电子的影响——电子再分布

得益于科学史上众多伟大思想家的不懈努力，我们如今对塞贝克效应等物理现象有了更为深入的理解。虽然详细探讨热电效应背后的理论超出了本文的范畴，但一个简化的直观解释足以让我们对这种效应有一个基本的认识。

如今我们知道，电场或者热能能够将导体价带中的一些电子释放到导带中。价电子由于与原子结合得过于紧密，无法对电流产生贡献，而导带中的电子则拥有足够的能量在材料中自由移动。当金属棒的两端存在温差时，热区会产生更多的自由电子。并且，热端的电子比导体冷端的电子受到更多的热搅动，这些热搅动的电子扩散速度比低能电子更快。

导线热端中较高浓度的热搅动电子会促使电子从热端向冷区扩散。由于这种热诱导的电子扩散，与导体的另一端相比，热区会带上正电。图2清晰地展示了温差是如何重新分配电子，并使它们从较热的区域移动到较冷的一端的。

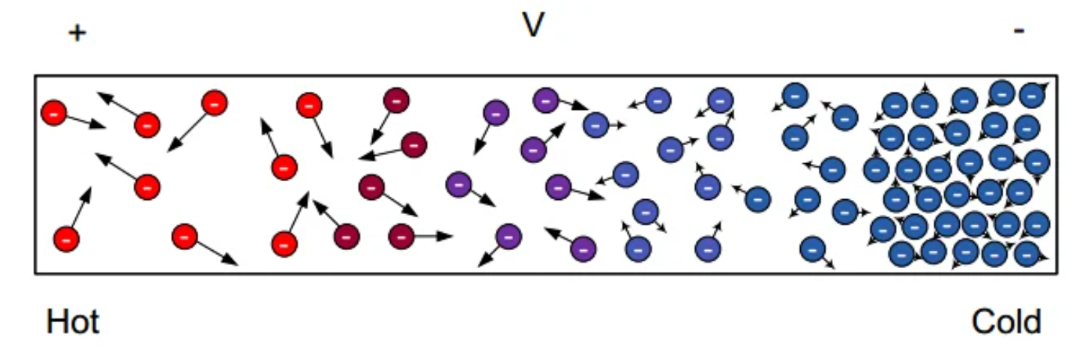
（图注：概述温差如何影响从热到冷的电子分布。图片由TI提供。）

那么，这种电子的再分配会持续多长时间呢？产生的热电压会试图产生与热感应电流方向相反的电流。随着越来越多的电子从较热的一端移动到较冷的一端，导线两端产生的热电压会越来越大。当热电压大到足以抵消温度引起的电子扩散时，就达到了一种平衡状态。此时，通过导体的净电流将为零。

塞贝克电压——塞贝克系数

沿导线的温度梯度产生的开路电压被称为塞贝克电压，这种现象就叫做塞贝克效应。在给定温差的情况下，产生的塞贝克电压取决于材料的特性。

为了评估给定材料中塞贝克效应的强度，我们定义了塞贝克系数。塞贝克系数的定义公式如下：

（图注：塞贝克系数定义公式）

其中，ΔV表示沿材料施加小温差（ΔT）所获得的电压差。需要注意的是，按照惯例，ΔV被定义为冷侧电压减去热侧电压。在图2所示的示例中，V冷-V热为负，这就导致塞贝克系数为负。我们稍后会更详细地讨论塞贝克系数的符号问题。

在上述公式中，假设ΔT较小。因此，我们还可以将塞贝克系数定义为产生的电压相对于温度的一阶导数：

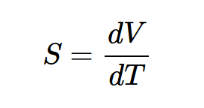
（图注：塞贝克系数的另一种定义公式）

塞贝克系数——绝对还是相对？

从上述两个公式中获得的值被称为绝对塞贝克系数，它指定了单个材料的塞贝克效应。例如，铝在0°C下的绝对塞贝克系数为-1.5μV/K。材料的塞贝克系数也可以表示为相对于参考材料的相对值。比如，铝的塞贝克系数可能会与铂相关，铂在0°C时的绝对值为-5μV/K。在这种情况下，铝的相对塞贝克系数为：

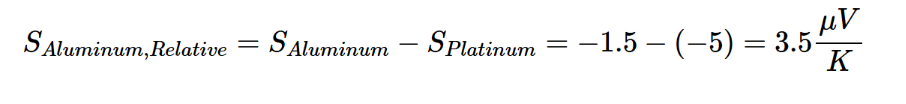
（图注：铝相对于铂的塞贝克系数计算示例）

图3给出了铝以及其他一些常见材料相对于铂的塞贝克系数。

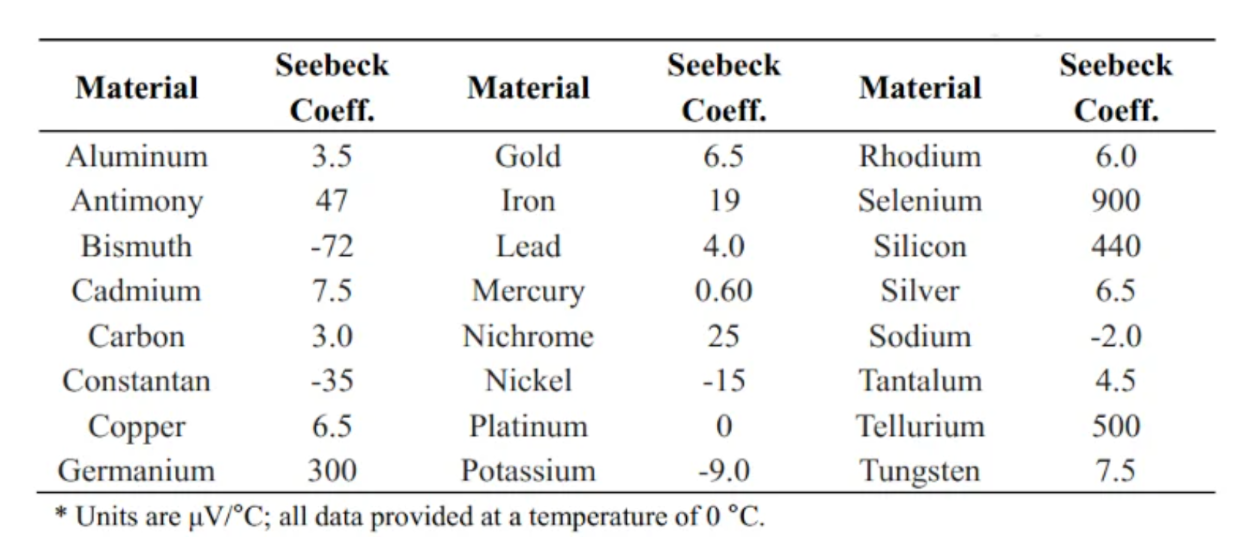
（图注：不同材料的塞贝克系数示例。数据由李提供。）

需要注意的是，材料的绝对塞贝克系数不能直接用万用表进行测量。这是因为电压表的引线（以及测量电路输入端的任何其他导电材料）会经历温度梯度并产生额外的塞贝克电压。以这种方式测量的电压将取决于被测材料以及测量电路中使用的材料的塞贝克效应。不过，绝对塞贝克系数可以通过应用塞贝克系数的开尔文关系来确定。而通过测量热电偶电路的输出，则可以很容易地确定相对值。

塞贝克效应的温度依赖性

塞贝克系数是温度的函数。图4清晰地展示了铂（Pt）和铌（Nb）的绝对塞贝克系数随温度变化的情况。