相位裕度的确定

运算放大器的环路稳定性通常通过相位裕度来衡量。相位裕度指的是当输出闭环增益低于单位增益时，输出信号相移相对于360度的差值。每个运算放大器都存在固有偏移，如主极点偏移，而额外偏移则取决于具体应用和放大器周围的元件。

不同的经验法则建议采用30度、45度甚至60度的相位裕度，那么究竟多大的相位裕度才能确保可靠的性能呢？对于传统的米勒补偿运算放大器，我们可以通过仿真来研究典型工艺差异对相位裕度的影响。

图1近似计算了具有1MHz单位增益带宽且Zo=300Ω的运算放大器的开环增益(Aol)和输出阻抗(Zo)。由于工艺差异，米勒电容(C26)的值会在约±30%的范围内变化，并且在整个温度范围内还会有额外±30%（近似值）的变化。这种变化造成的总误差为±39%。由于米勒电容的容值会改变运算放大器Aol中主极点的位置，进而显著影响单位增益带宽和相位裕度，所以这些规格通常仅作为典型值给出，即使是精密放大器和高速放大器也是如此。

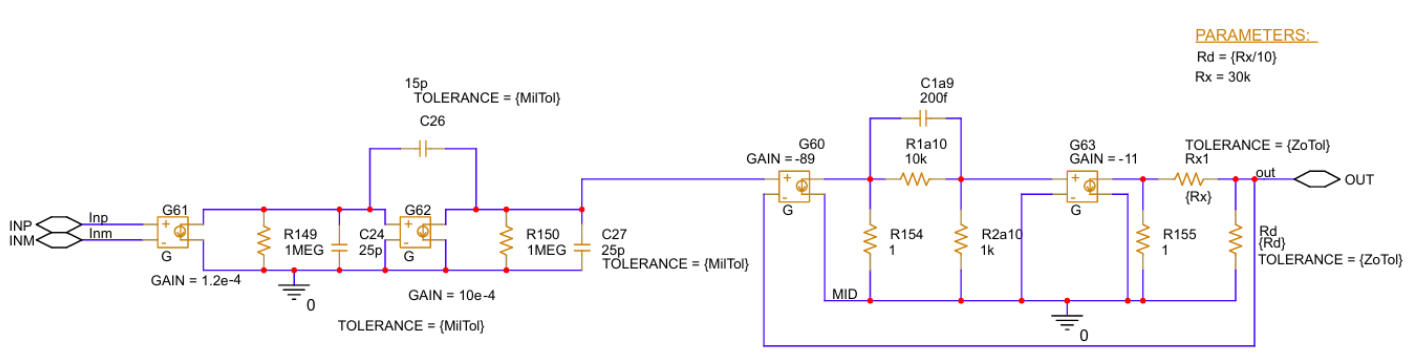
图1开环增益和输出阻抗PSpice^{®}forTI电路

图1中的放大器由负载电阻和电容进行设置，使反馈环路具有45度的相位裕度。通过对影响环路稳定性的主要因素，如米勒电容器、开环输出阻抗和放大器周围的无源器件进行MonteCarlo分析，可以估算工艺差异和温度变化对电路相位裕度的影响程度。

图2展示了蒙特卡洛分析产生的相位裕度。本分析对米勒电容器施加了±40%的变化，对Zo施加了±15%的变化，对负载电容器施加了±10%的变化，对负载电阻器施加了±5%的变化。这些是米勒电容器和Zo的预期内部容差，以及许多通用应用的典型元件精度。

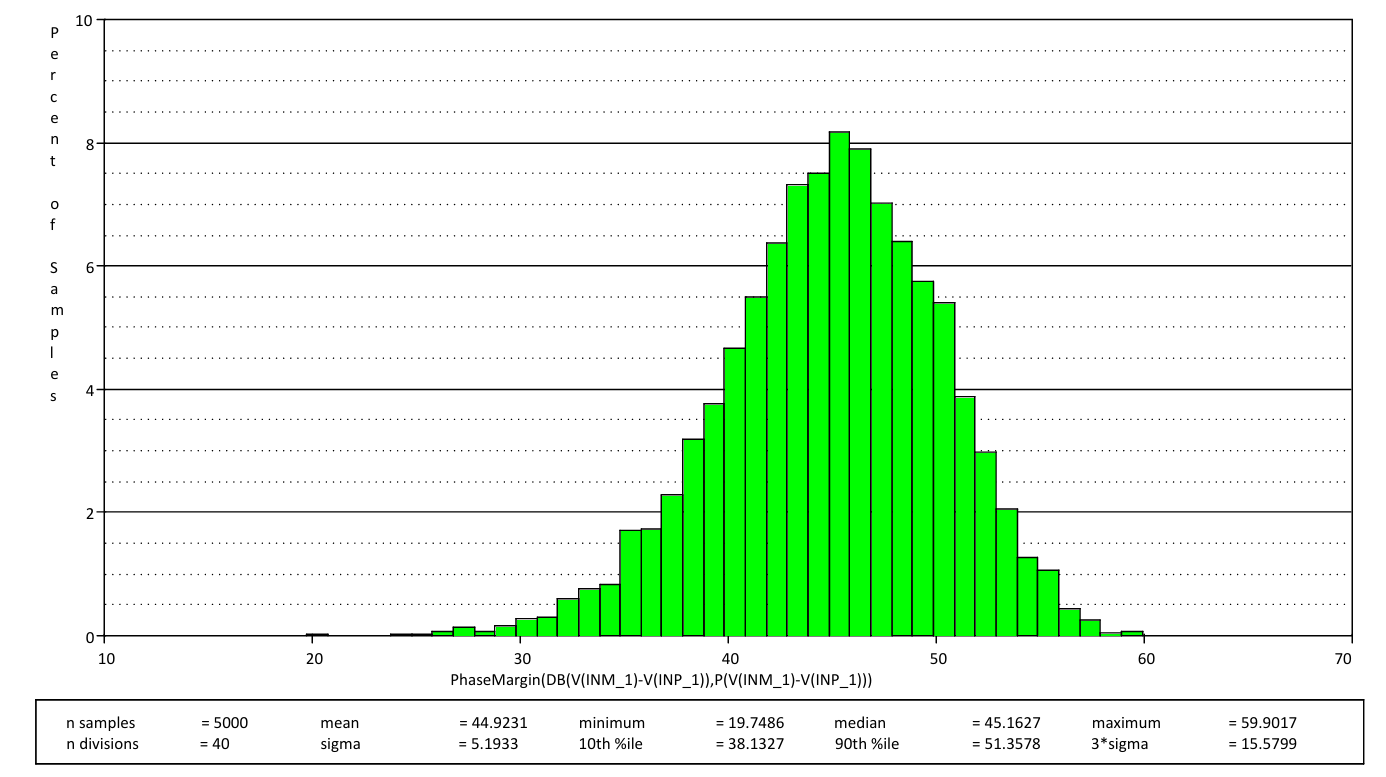
图2针对估计的工艺差异和温度变化进行5,000次蒙特卡洛分析

在该变化范围内，反馈环路的相位裕度最小为19度，与45度相差26度。在工艺差异和温度范围内，如果电路具有大约27度的相位裕度，则电路将保持稳定，不过45度的相位裕度可提供良好的瞬态性能和稳定时间。相位裕度越接近0度，输出将越偏离最终值，稳定到最终输出值所需的时间就越长。45度的相位裕度可提供足够的设计容差，允许相位裕度发生一定变化而不影响稳定时间或出现大量过冲。

需要注意的是，虽然这些仿真有助于了解米勒电容器变化对性能的影响，但最终电路设计人员需要对设计的性能负责。因为仿真的精确度仅与所包含的非理想属性相关，为了降低计算的密集度，往往会假设许多理想属性。

补偿方案

在某些情况下，由于电压轨调节、模数转换器的滤波电容或其他电路需求，无法减小运算放大器输出端的电容器。此时，如何实现适当的相位裕度呢？有多种补偿方案可以提高相位裕度，本文重点介绍两种方案，即隔离电阻器(R_{iso})和R_{iso}双反馈，如图3和图4所示。在设计这些电路时，确定所需的R_{iso}值以稳定反馈环路可能具有一定难度。

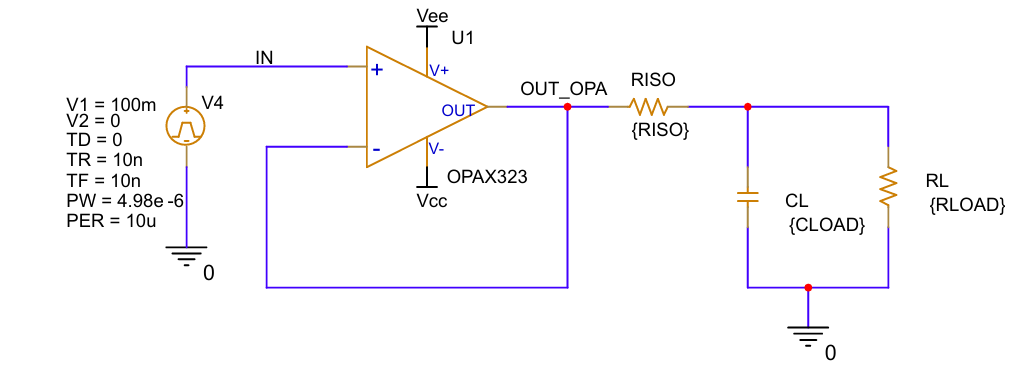
图3R_{iso}补偿方案

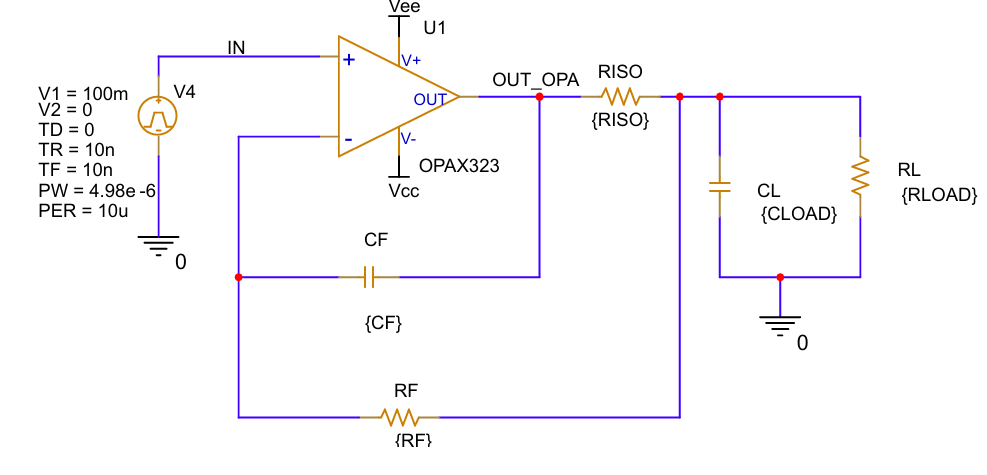
图4R_{iso}双反馈方案

R_{iso}是隔离由负载电容引入的相位滞后的简单方法，具体做法是在反馈环路和负载电容器之间放置一个电阻器。但该方法存在一个缺点，即当输出有负载电流时，直流精度会降低。直流误差的大小等于隔离电阻器的值乘以输出电流。

R_{iso}双反馈补偿方案克服了这种直流误差。该电路启用了通过反馈电容器的高频路径来稳定反馈环路，并启用了直流路径，允许运算放大器补偿隔离电阻器上的I×R压降。设计人员可以通过数学方法或仿真方法来求出这些值，具体做法是尝试不同的R_{iso}值并查看哪个值可以实现稳定运行。

对放大器环路稳定性进行精确建模涉及开环增益和开环输出阻抗两个主要因素。德州仪器的标准运算放大器宏模型Green-Williams-Lis(GWL)为2016年之后发布的所有运算放大器准确表征了这些参数。许多更受欢迎的运算放大器，如LM2904及其更新版本LM2904B，也具有为其创建的GWL宏模型。SPICE宏模型的库文件包含一个头文件，详细说明了在SPICE模型中准确反映的参数。如果对开环增益和开环输出阻抗进行准确建模，模型的稳定性很可能会反映器件的实际性能。

确保SPICE模型的精度可以使设计人员分析电路的环路稳定性，并以数学方式计算R_{iso}的理想值。确保45度相位裕度的R_{iso}值应在反馈环路中的反馈因子(1/β)和放大器开环增益交点处产生零点。为了进一步确保这一点，可以在开环增益为20dB的位置设置零点，此时可以看到反馈环路中由零点引入的最大正相移。

表1列出了用于计算R_{iso}双反馈的隔离电阻值和反馈分量的公式：

PSpiceforTI的强大功能之一是可以设置、存档和共享仿真及公式以供后续原理图使用。由于R_{iso}和R_{iso}双反馈的评估是公式化的且易于重复，设计人员可以利用这些模板工程，而无需记住在四种常见运算放大器电路上计算R_{iso}或R_{iso}双反馈电路的的公式。只需下载PSpiceforTI工程，放入要分析的运算放大器，输入用于完成需要稳定的特定电路的参数，然后运行仿真以找到所需的适当R_{iso}值。这些工程还可以补偿因反相端子上的电容而不稳定或具有极大反馈电阻的电路。

直接替代式解决方案

对于不需要额外补偿电路，或者添加补偿电路不可行的情况，德州仪器的OPA994器件系列提供了一种解决方案。该器件系列具有一个在整个容性负载范围内都保持稳定的特殊补偿结构。这是因为当输出看到不同的容性负载时，器件的带宽会发生变化。通过保持带宽始终低于输出阻抗和容性负载引入的极点，无论在输出端放置何种电容器，都能保持放大器的稳定性。图5展示了在不使用外部补偿电阻器的情况下，不同负载电容值对应的相位裕度，该图取自OPA994数据表。

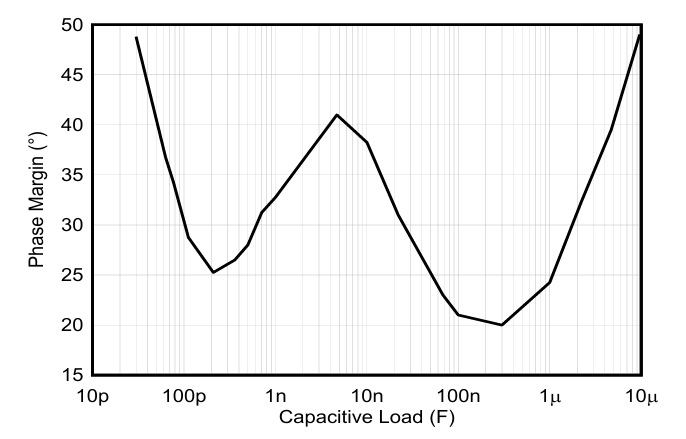
图5各种容性负载对应的相位裕度（单位增益下）

然而，每一种设计决策都有其成本和优势，OPA994器件系列也不例外。设计越复杂，器件就越大，可能比简单的器件更昂贵。此外，该器件无法集成到德州仪器的超小型封装中，例如0.64mm²Extra-SmallOutlineNo-Lead(X2SON)封装。此设计目前仅在双极放大器中可用，因此如果需要互补金属氧化物半导体(CMOS)的低输入偏置电流，该器件可能具有过高的输入偏置电流。

与CMOS器件相比，双极放大器具有许多优势，包括更低的噪声、更大的带宽以及更低的静态电流。设计人员可以根据具体电路对双极与CMOS进行全面权衡。总体而言，OPA994在许多情况下可用作“即插即用”解决方案，以实现稳定性。

结语

在运算放大器的初始设计阶段，首要问题是确定多大的相位裕度足以在工艺差异和温度范围内实现可靠的性能。如果初始实现的相位裕度不够，可以采用多种补偿方案将相位裕度增加到可接受的水平。这些解决方案可以通过PSpiceforTI中预配置且易于使用的工程来实现。最后，如果已投入生产的工程确实存在稳定性问题，可以考虑使用建议的直接替代式解决方案。通过对这些问题的深入研究和合理应用，设计人员能够更好地解决运算放大器的稳定性问题，提高电路的性能和可靠性。